
时间:2022-07-01 09:01:34来源:网络整理
简介
高阶交互无处不在且很重要,从社交网络中的信息传播、神经元网络的放电行为到生态系统中多个物种的交互。然而,现有的研究工作假设高阶结构是已知的。在社会、生物、信息等一些复杂系统中,我们往往只能观察状态数据,很难获得结构信息。因此,基于观测数据重构网络结构是研究复杂系统的重要途径。然而,以前的重建工作主要集中在具有成对或两体交互的网络上。如何从观测数据中重建具有高阶关系的网络?本文初步尝试用简单的复杂结构重构网络。
为探索高层互动结构,聚焦网络科学前沿,集智社推出“高层次网络读书会”,学习分享相关研究成果。读书会从6月28日开始,为期10-12周,将邀请Ginestra Bianconi等一线学者做报告。欢迎从事复杂网络研究和应用的朋友加入。详情见文末。
研究领域:高阶网络、网络重构、单纯复形
论文题目:
从二元传染和伊辛数据完全重建单纯复形
论文链接:
/articles/s41467-022-30706-9
1.简单复杂重构必要性研究
网络在现实世界中无处不在,但它们的特定拓扑结构和控制网络属性和物理可观察性的内在动力学通常是未知的。目前,一种可行的方法是从观测数据中找到网络拓扑和节点动力学方程,但该领域的先前工作主要集中在仅具有成对交互的传统网络上。然而,许多复杂系统不能仅用成对连接来表示。
例如,在社交网络中,一个新产品由多个朋友共同推荐通常比一个朋友的推荐更有说服力,从而使个人有更强的购买新产品的意愿;在谣言传播过程中,如果一条虚假消息被多人同时分享或宣传,很可能会被个人相信;或者在描述科学家之间的合作时,pairwise connections 只能描述哪两个作者合作,而不是当论文中出现多个作者时的科学情况。因此,二元网络无法捕捉群体的影响,需要超越成对关系的高阶网络来描述群体动态影响个体行为的复杂方式。
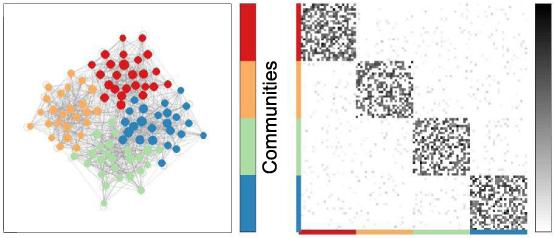
单纯复形是一种特殊的高阶网络,它是集合的集合,也构成单纯形。例如,在一个科学家合作网络中,如果三个作者形成一个2-单纯形,说明这三个作者有合作关系,那么任何两个作者也有合作关系,那么这两个作者也会形成一个1-单纯形。形状。
可见,高阶网络比传统网络能更全面、更准确地描述真实系统。基于此,如何从观测数据中推断出这种特殊的高阶网络结构-单纯复形具有特别重要的意义和价值,这将是一个具有挑战性和重要的科学问题。
图1单纯形图
2.重构单纯复形的整体框架
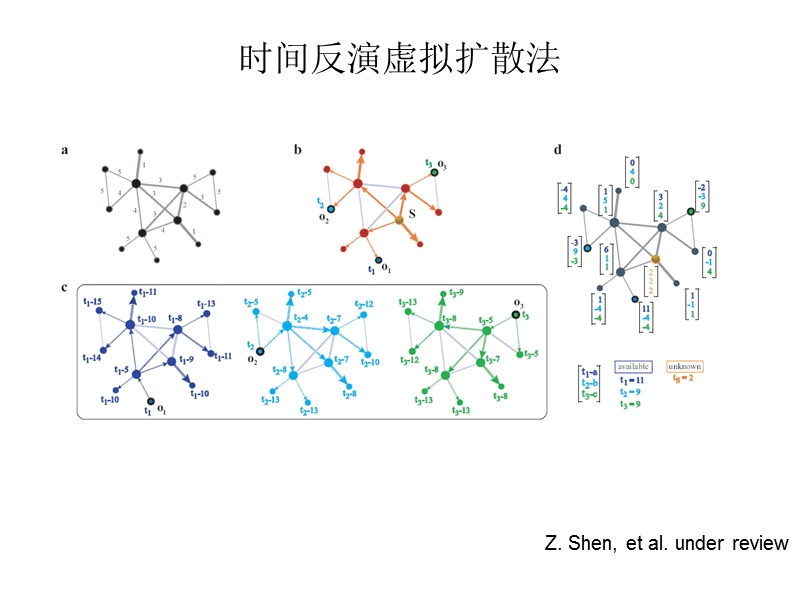
在安徽大学张海峰团队最新发表在Nature Communications上的著作中,为了解决单纯复形重构问题,作者从最简单的单纯复形网络(2-单纯复形)入手,采用基于社会的在传染动力学和单纯形Ising动力学两种模型生成的二进制时间序列数据上,设计了一种纯数据驱动的方法,基于统计推理框架重构2-单纯形复杂网络。其中,在数据生成过程中,为了体现多体结构的存在,两种动力学模型有一个共同点:在考虑两个体之间的相互作用的同时,也注重两者之间的协同强化作用。三具尸体。
接下来,我们的目标是完全重构对交互和 2-simplex,即确定每个节点所属的 1-simplex 和 2-simplex。重构过程可以分为以下三个步骤:(1)根据观测数据构建似然函数;(2)根据EM的思想(Expectation-Maximization)最大化似然函数) 方法,获取三体交互的二体和连通概率;(3)执行改进的两步重建策略,显着提高重建效率。
让我们详细看一下重建方法的三个步骤。第一步,将这个问题通过统计推断的方式转化为似然函数最大化问题,即借助条件概率公式,可以写成个体i的状态翻转为被刺激的概率由任何其他单个个体和被任何两个个体的协同强化刺激的概率,然后根据每个时间步的翻转次数的期望,个体 i 被感染的次数的似然函数可以获取时间段。
第二步,根据EM方法的思想,估计每个节点和重构节点形成二体的概率以及任意两个节点和重构节点形成三体的概率。理论上,可以通过截断概率值得到重构结果。但是不难发现,仅使用前两步进行重构的效率很低,其复杂度主要来自于2-simplex的预测,因为在预测每个节点所属的2-simplex时,需要计算
概率值。
因此,第三步利用单纯复形本身的性质,提出了改进的两步重构策略,首先预测每个节点的“近似”邻居,提取预测邻居的时间序列;然后仅基于提取的时间序列,可以进一步有效地预测每个节点所属的二体和三体交互。
图。图2 基于社会传染动力学数据重构2-单纯形复合体的总体框架示意图。 (a)-(e) 基于统计推断方法的直接重建过程。 (a)(b)(f-i) 根据修改后的两步重构策略的重构过程。
为了验证重建方法的效果,基于社会传染动力学数据和单纯形伊辛动力学数据,我们分析了三个合成的 2-单纯形复合体(ERSC、SFSC、SWSC)和四个真实数据的 2-重构该集合构造的单纯形复合体(Hypertext2009、Thiers12、InVS15、LyonSchool)。同时考虑了二体和三体密度、网络规模、传播速率、事件个数等因素对重建结果的影响。
研究结果表明,该方法可以高效地重构网络中的二体和三体关系,验证了重构方法的鲁棒性。此外,与直接重建的一步法相比,两步法重建策略显着减少了计算时间加权网络,复杂网络,科学家合作网络,层次加权,同时提高了重建精度。
图。图 3 基于社会传染动力学数据的四个真实 2-单纯形复合体 (a-d) 和重建性能 (e-h) 的可视化。
3.期待高阶网络重构
网络重构问题是网络科学研究的热点问题。对于高阶网络的重构,还有很多悬而未决的问题。
例如,这项工作的重构框架是从社会传染动力学和单纯形伊辛动力学的二进制时间序列数据中制定的,如何从更一般的动力学产生的数据中重构高阶网络结构值得研究;这种统计推断方法是针对传统网络之外“最简单”的网络结构——2-单纯形图等)而开发的,是一个值得研究的课题;此外加权网络,复杂网络,科学家合作网络,层次加权,如何利用较短的时间序列数据来提高重构精度也是一个值得考虑的问题。我们希望这项工作能够促进对高阶网络重建这一新兴子领域的进一步研究。
王欢 |作者
邓一学 |编辑器
声明:文章仅代表原作者观点,不代表本站立场;如有侵权、违规,可直接反馈本站,我们将会作修改或删除处理。
图文推荐

2022-07-01 09:01:34

2022-06-30 10:01:47
2022-06-30 09:01:30

2022-06-29 12:01:57
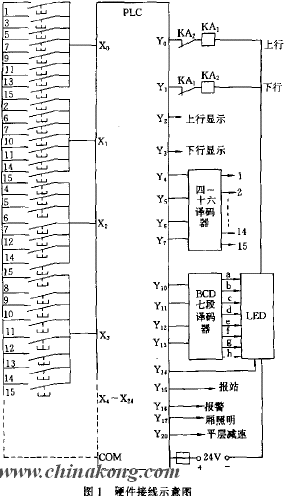
2022-06-28 13:01:43
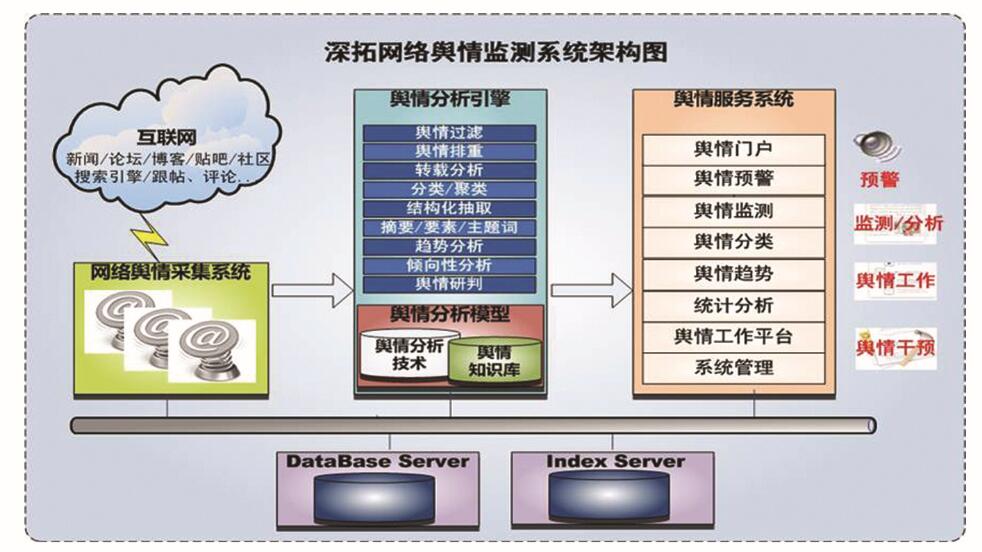
2022-06-26 12:04:38
热点排行
精彩文章
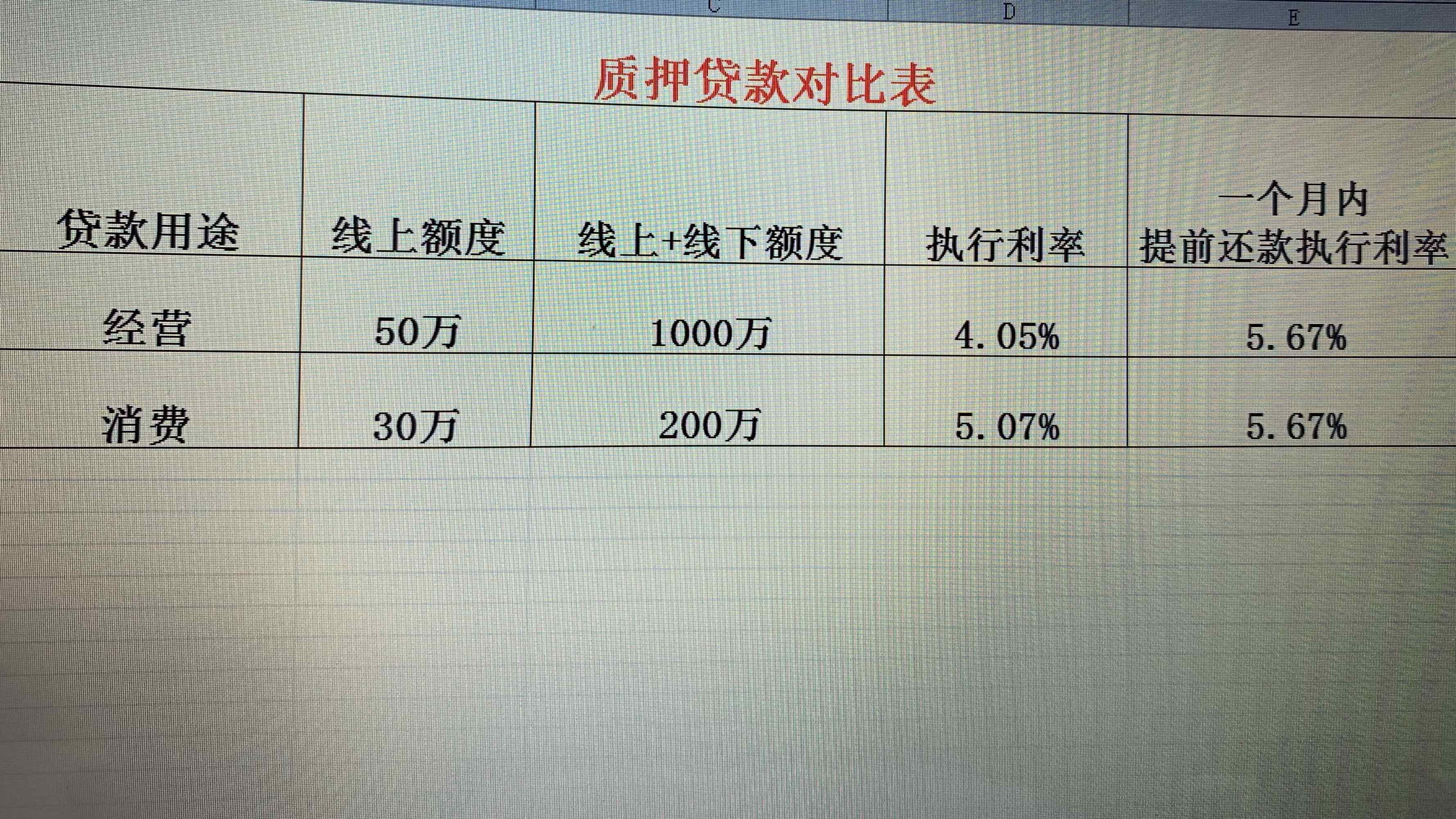
2022-06-30 13:00:32

2022-06-30 12:00:43

2022-06-30 11:00:41

2022-06-30 10:01:40
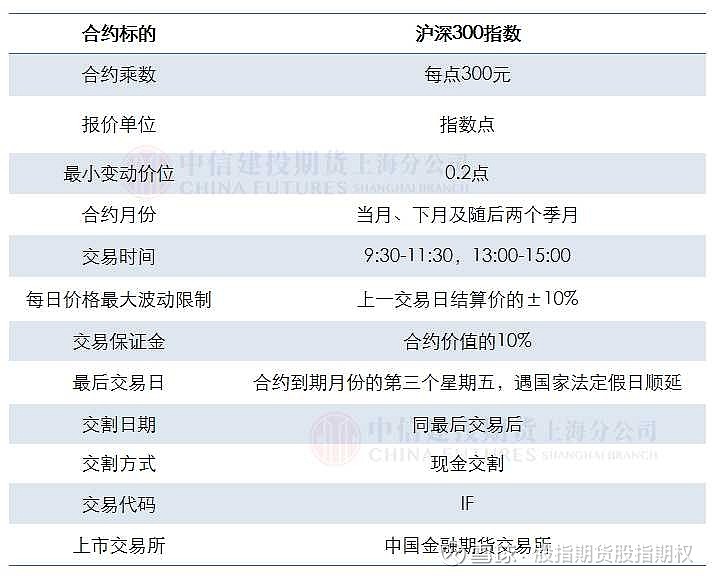
2022-06-30 09:00:54

2022-06-29 14:02:19
热门推荐
